T Test

What Is a T-Test (Definition)?

A t-test is an inferential statistic that is used to examine if two groups that are related in some way have a significant difference in their means. It’s most commonly used when data sets, such as those obtained by flipping a coin 100 times, are expected to follow a normal distribution and have unfamiliar changes. 

The t-test is one of several statistical tests used to evaluate hypotheses. To evaluate statistical significance, a t-test examines the t test statistics, t-distribution values, and degrees of freedom. An analysis of variance must be used to perform a test with three or more means.

When to use a T-Test?

When comparing the mean of two samples, a t-test is used. A t-test supposes that the sample has a normal distribution. When the population characteristics (mean and standard deviation) are unknown, a t-test is used. The t-test is a parametric difference test, which means it is based on the same data assumptions as other parametric tests. The t-test is predicated on the following data assumptions:

• are independent.
• have a (roughly) normal distribution.
• Each group being compared has the same level of variance.

If your data does not satisfy these assumptions, a nonparametric alternative to the t-test, such as the Wilcoxon Signed-Rank test for data with uneven variances, can be used instead.

What type of T-test should I use?

You must consider two factors when choosing a t-test: whether the groups being compared are from the same population or two different populations, and whether you want to test the difference in one direction or the other. And if you want to consider it on the other hand with the basic priorities and alpha value. 

One-Sample, Two-Sample, or Paired T-Test?

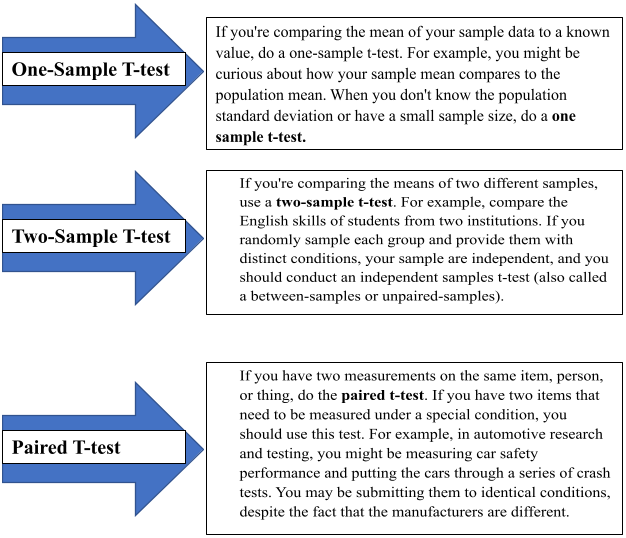
One-Tailed or Two-Tailed T-Test?

• A one-tailed t-test can be used to determine whether one population mean is bigger than or less than the other. A one-tailed test uses all of your alpha to evaluate the statistical significance in the one direction of interest if you use a significance level of.05. This indicates that 0.05 is in one tail of your test statistic’s distribution. When you use a one-tailed test, you’re looking for a relationship in one direction while completely discounting the chance of a relationship in the other.
• Perform a two-tailed t-test if the two populations are different. A two-tailed test uses half of your alpha to test statistical significance in one direction and half of your alpha to test statistical significance in the other direction if your significance is 0.05. This signifies that 0.025 is in each tail of your test statistic’s distribution. When you do a two-tailed test, you are testing for the probability of the link in both directions, regardless of the direction of the relationship of your hypothesis.

What is the Difference between a One-Sample T-Test and A Paired T-Test?

What Does a T-Test Measure?

A t-test is an inferential statistic that is used to determine whether there is a significant difference between the means of two related groups. In this approach, it creates a number (the t-value) that shows the magnitude of the difference between the two-group means being compared, as well as the probability that this difference occurs only by chance (p-value).

Which T-Test Should I Use?

Whether you’re investigating one group or two, and whether you care about the direction of the difference in group means, will determine the t-test you use. Use a paired t-test to compare the group mean over time or after an intervention if you’re only studying one group, or a one-sample t-test to compare the group mean to a standard value if you’re only studying one group. Use a two-sample t-test if you’re comparing two groups. Use a two-tailed test if you only want to know if there is a difference. Use a one-tailed test to see if one group’s mean is higher or lower than the other.