Regression Analysis
What is Regression Analysis?
Regression analysis is a statistical technique used to determine the relationship between two or more variables. It studies the effect of one or more independent variables on a dependent variable.
Formula
| = | dependent variable | |
| = | function | |
| = | independent variable | |
| = | unknown parameters | |
| = | error terms |
Key Types of Regression Models:
- Linear Regression – Used to model linear relationship between dependent and independent variables. Most commonly used.
- Logistic Regression – Useful when the dependent variable is categorical. Helps determine odds of an outcome.
- Polynomial Regression – Models non-linear relationships using polynomial terms. Flexible for complex data.
- Stepwise Regression – Identifies most significant predictors in sequential steps based on statistical criteria.
Uses of Regression Analysis:
- Determine strength of effect that independent variables have on a dependent variable.
- Forecasting trends and making predictions.
- Provides deeper insights for better decision making.
- Helps test theories and causal relationships between variables.
- Assess impacts of policy changes on economic indicators.
- Identify trends and growth patterns.
Relevance in Economics Research:
Regression is extensively used in economics to build forecasting models analyzing historical relationships between economic factors. For example, modeling inflation rates based on interest rates, money supply etc. It is pivotal for data-driven policy formulation and business decision optimization across sectors.
With ability to incorporate multiple complex variables, regression enables modeling real world economic phenomena for predictive insights vital for planning and strategy.
Regression Analysis
The link between dependent and independent variables is measured using regression analysis, which is a predictive modelling technique. Regression analysis can be used for forecasting, time series modelling, identifying the relationship between variables, and predicting continuous values. We can use regression analysis to analyze data and model data.
Regression Line
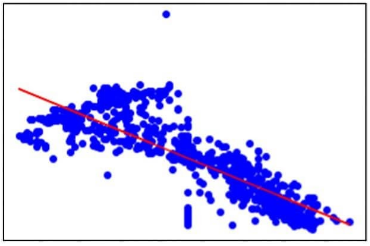
A Real-World example of how Regression Analysis is used
A simple linear regression real-world example may involve determining a link between revenue and temperature, with revenue as the dependent variable and a sample size for revenue. Multiple variable regression can be used to identify the relationship between temperature, pricing, and the number of workers and revenue. Regression analysis is a technique for identifying patterns in data. For instance, you might think there’s a link between how much you eat and how much you weigh. Regression analysis might help you prove it.
Another example: A graduating student must select the faculty and university degree program in which he or she will attend. Perhaps he has already found a field for his future career. Perhaps a long-standing family custom instructs him or her to follow in the footsteps of his or her parents. In these instances, the degree of uncertainty in making a decision will be considerably reduced. On the other hand, if the student does not have true vocations or is not particularly tuned to specific choices, he or she may be interested in learning more about the graduates’ professional achievements. In this case, a statistical analysis of graduate data from past years could help him or her in making a decision.
General Uses of Regression Analysis
Regression analysis is a method of predicting future events between one or more independent variables and a dependent (goal). Time series modelling and determining the cause-and-effect relationship between variables are some of the most common applications of regression analysis. Machine learning and regression share a lot of similarities. This statistical method is utilized in a variety of industries, including:
- Financial industry: know stock price trends, estimate prices, and evaluate risks in the insurance area.
- Marketing: determine the effectiveness of market campaigns, forecast pricing, and product sales.
- Manufacturing: analyze the relationship of variables that affect a better engine’s performance.
- Medicine: predict various combinations of drugs in order to prepare generic treatments for disorders.
Types of Regression
There are many different types of regression analysis procedures, and the number of components determines which method to utilize. The type of dependent variable, the form of the regression line, and the quantity of independent variables are all considerations to consider. Three types of regression analysis approaches are often used to solve the regression problem using machine learning: linear regression, logistic regression, and polynomial regression. They are the most often used regression approaches.
The following are the many regression techniques:
- Linear Regression
- Logistic Regression
- Polynomial Regression
- Ridge Regression
- Poisson Regression
- Quasi Poisson Regression
- Lasso Regression
- Negative Binomial Regression
- Support Vector Regression
- Bayesian Linear Regression
- Cox Regression
- Elastic Net Regression
- Ordinal Regression
- Tobit Regression
- Partial Least Regression (PCR)
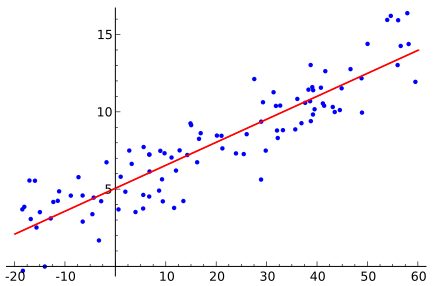
Linear Regression
In machine learning, linear regression is one of the most basic types of regression. A predictor variable and a dependent variable are connected linearly in the linear regression model. When there are numerous independent variables in the data, linear regression is referred to as multiple linear regression models.
The linear regression model is represented by the equation y=mx+c+e, where m is the slope of the line, c is an intercept, and e is the error in the model.
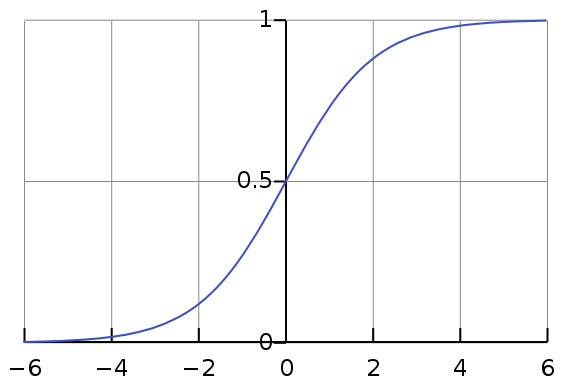
Logistic Regression
When the dependent variable is isolated, one of the types of regression analysis techniques used is logistic regression. For instance, 0 or 1, true or false, and so forth. This means the target variable can only have two values, and the relationship between the target variable and the independent variable is represented by a sigmoid curve.
In Logistic Regression, the Logit function is used to determine the connection between the target variable and the independent variables. The logistic regression is represented by the equation below. Logit (p) = ln (p/1-p) = b0+b1X1+b2X2+b3X3+…+bkXk; where p is the feature’s probability of occurrence.
Polynomial Regression
Polynomial Regression is a form of regression analysis technique used in machine learning that is similar to Multiple Linear Regression but with a few differences. The link between independent and dependent variables, X and Y, is denoted by the nth degree in Polynomial Regression.
As an estimator, it is a linear model. In Polynomial Regression, the Least Mean Squared Method is also used. In Polynomial Regression, the best fit line that goes through all of the data points is a curved line that relies on the power of X or the value of n.
The Polynomial Regression is represented by this equation: l = β0+ β0x1+ꜫ
Although there are more types of regression analysis than those described here, these three are the most popular. If you choose the appropriate one, your data will be able to reach its full potential, putting you on the road to deeper insights.
What is Linear Regression?
Regression is a method for modelling and analyzing the relationships between variables, as well as how they contribute to and are connected to obtaining a specific outcome. In the linear regression heading above, you can see a detailed view of liner regression.
Simple Linear Regression
In machine learning, linear regression is the simplest fundamental type of regression technique. The model has a single parameter and a linear relationship between the dependent and independent variables. Multiple linear regression models are used when the number of independent variables is increased. The following equation is used to denote simple linear regression.
y = mx + c + e, where m is the line’s slope, c is the intercept, and e is the model’s error.
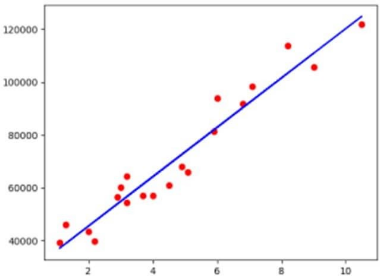
Changing the values of m and c for different combinations produces the best-fit decision boundary. It’s important to remember that a simple linear regression model is more inclined to outliers, hence it shouldn’t be utilized with large datasets. The independent and dependent variables should have a linear relationship. There is only one variable that is both independent and dependent. A best-fit straight line is the sort of regression line.
Multiple Linear Regression
A data scientist or data analyst can use simple linear regression to predict only one variable by training the model and predicting another variable. A multiple regression model, on the other hand, includes more than one variable. The following linear function, y = b0 + b1x1 is used in simple linear regression to predict the value of a target variable y, with an independent variable x.
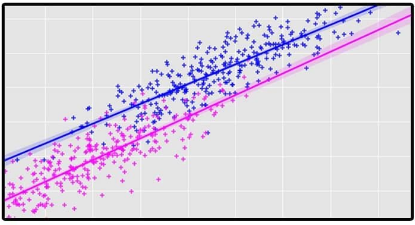
After fitting the linear equation to observed data, we obtain the parameters b. that best suits the data to minimize the square error. Multiple regression displays the characteristics of multicollinearity, autocorrelation, and heteroscedasticity. Multicollinearity raises the variance of coefficient estimations and makes them extremely sensitive to small model modifications. As a result, the coefficient estimations are unreliable. We can use a forward selection, backward elimination, or stepwise strategy for feature selection when there are several independent variables.
We glad you enjoyed this post informative and you are now confident in your ability to address comparable challenges using regression analysis. Although if your assignments seem to be difficult, you can still get statistics assignment help from Assignment Studio to finish your regression assignments just before deadlines.
Why Regression Analysis Matters in USA Assignments?
1. Unraveling Complex Relationships: Regression analysis is the key to deciphering complex relationships between variables. Whether exploring economic trends, social patterns, or scientific phenomena, understanding regression analysis is pivotal for USA students tackling diverse assignments.
2. Validating Hypotheses: In the rigorous academic environment of the USA, assignments often require hypothesis testing. Regression analysis provides a robust framework for validating hypotheses, ensuring the credibility of your research and analysis.
3. Real-world Application: Beyond the classroom, regression analysis is extensively applied in various fields across the USA. From business analytics to healthcare research, mastering regression equips you with skills applicable to real-world problem-solving.
How Our Support Enhances Regression Analysis in Your Assignments
1. Customized Guidance: At [Your Academic Help Website], we provide customized guidance tailored to the specific requirements of your assignments. Whether it’s simple linear regression or more complex multiple regression models, our experts ensure you grasp the nuances effectively.
2. Application in Diverse Disciplines: Our support spans across disciplines. Whether you’re working on economics, sociology, psychology, or any other field, our team specializes in applying regression analysis to diverse academic contexts relevant to the USA’s educational standards.
3. Hands-on Learning: We believe in hands-on learning experiences. Our approach involves practical examples and real-world scenarios to ensure that you not only understand regression analysis theoretically but can also apply it confidently in your assignments.
1. Economics Assignment: Predicting Unemployment Rates
Scenario: In an economics assignment, students may use Regression Analysis to predict unemployment rates based on various economic indicators such as GDP growth, inflation rates, and government spending. The assignment could involve collecting historical data, building a regression model, and interpreting the coefficients to understand the impact of each variable on unemployment.
2. Marketing Assignment: Analyzing Sales Performance
Scenario: For a marketing assignment, Regression Analysis can be applied to analyze the factors influencing sales performance. The students might explore variables like advertising spending, product pricing, and competitor activities. The goal is to build a regression model that helps the marketing team make informed decisions to maximize sales.
3. Health Sciences Assignment: BMI and Heart Disease Risk
Scenario: In a health sciences assignment, students might use Regression Analysis to study the relationship between Body Mass Index (BMI) and the risk of heart disease. By collecting data on BMI levels and corresponding incidences of heart disease, the analysis aims to quantify the association and provide insights into the health implications of varying BMI values.
4. Finance Assignment: Stock Price Prediction
Scenario: For a finance assignment, Regression Analysis can be applied to predict stock prices based on relevant financial variables. Students might examine factors such as company earnings, market trends, and interest rates to create a regression model that forecasts future stock prices. This exercise helps in making investment decisions.
5. Sociology Assignment: Factors Affecting Crime Rates
Scenario: In a sociology assignment, Regression Analysis can be employed to understand the factors influencing crime rates in a given region. Variables such as unemployment rates, education levels, and law enforcement spending can be analyzed to build a regression model that sheds light on the socio-economic determinants of crime.
6. Environmental Science Assignment: Impact of Pollution on Public Health
Scenario: In an environmental science assignment, students might use Regression Analysis to investigate the relationship between pollution levels and public health outcomes. By collecting data on air or water quality and health indicators, the analysis aims to quantify the impact of pollution on the well-being of the population.
These examples illustrate how Regression Analysis can be applied across diverse academic disciplines to analyze relationships between variables, make predictions, and derive meaningful insights. The methodology enhances the depth and credibility of assignments, showcasing the practical applicability of Regression Analysis in real-world scenarios.
Popular assignments where regression analysis is extensively applied
Economics Assignments
- Econometrics (ECON251)
- Forecasting Models & Analysis (ECON301)
- Time Series Analysis (ECON352)
- Development Economics (ECON451)
Statistics Assignments
- Statistical Inference (STAT101)
- Linear Regression Models (STAT201)
- Multivariate Statistical Analysis (STAT301)
- Big Data Analytics (STAT451)
Marketing Assignments
- Marketing Research Methods (MKT301)
- Consumer Behavior Analysis (MKT431)
- Digital Marketing Analytics (MKT415)
Finance Assignments
- Investments & Portfolio Analysis (FIN311)
- Fixed Income Securities Valuation (FIN331)
- Risk Analysis & Modeling Techniques (FIN402)
Healthcare Assignments
- Biostatistics (BIOS301)
- Epidemiology Data Analysis (EPI412)
- Health Trends & Surveillance (PUBH401)
Highlighting these course codes helps connect assignments with appropriate regression-based data analysis techniques across fields.
We offer expert Regression Analysis Assignment Help tailored to your academic needs. Our seasoned statisticians guide you through the intricacies of Regression Analysis, ensuring a clear understanding of concepts and impeccable solutions. Whether it’s economics, marketing, health sciences, or any other discipline, our customized approach guarantees accuracy and relevance. Benefit from hands-on learning, timely delivery, and real-world application of Regression Analysis. Excelling in your assignments has never been this accessible. Contact us today and elevate your academic journey with our top-notch Regression Analysis Assignment Help services!
FAQs
What are some types of regression analysis?
Common types include linear regression, logistic regression, polynomial regression, ridge regression, lasso regression, stepwise regression, and multiple regression. Each technique serves a different analytical purpose.
What is linear regression?
Linear regression is used to model a linear, straight-line relationship between dependent and independent variables. It is based on minimizing the differences between observed and predicted values.
How to determine which variables to include in a regression model?
Start will all potential factors then eliminate variables one by one that are not statistically significant based on p-values while ensuring the model still explains majority of dependent variable changes.
What are limitations of regression analysis?
It determines correlations and not causations. Extreme outliers can skew results. Only models linear relationships well. Sensitive to collinear variables. Residuals must be checked to validate model quality.
What is a good R-Squared value?
R-squared indicates what percentage of variation in dependent variable is explained by the regression model. Generally 0.6 and higher (max 1) indicates well-fitted models.



