Regression Models using Cross Section Data
Regression Models
Regression Models using Cross Section Data: Use the data set in DATA_ASSIGNMENT which contains information on number of medals won by each country between 1960 and 1999 in the Olympic Games and the characteristics of these countries. Country ID is the country identifier. Year denotes the year when the Olympics games held. Real GDP is the Real Gross Domestic Product of a country in millions of dollars. Population is the number of people living in a country in millions of people. Total Medals in the sum of gold, silver and bronze medals won by a country. Host Country is a dummy variable that takes the value 1 if the country is hosting the Olympic Games and takes the value 0 if the country is not hosting the games. Planned Economy is a dummy variable that takes the value 1 if the country is a planned economy and is not a member of Soviet Union and 0 otherwise. Soviet Union Member is a dummy variable that takes the value 1 if the country is a member of Soviet Union and takes the value 0 if the country is not a member.
- Present the descriptive statistics of the variables Real GDP, Population, Total Medals. Comment on the means and measures of dispersion of the variables.
- Estimate the following simple regression model of total medals on real GDP.
TotalMedals=β0+ β1realGDP+u
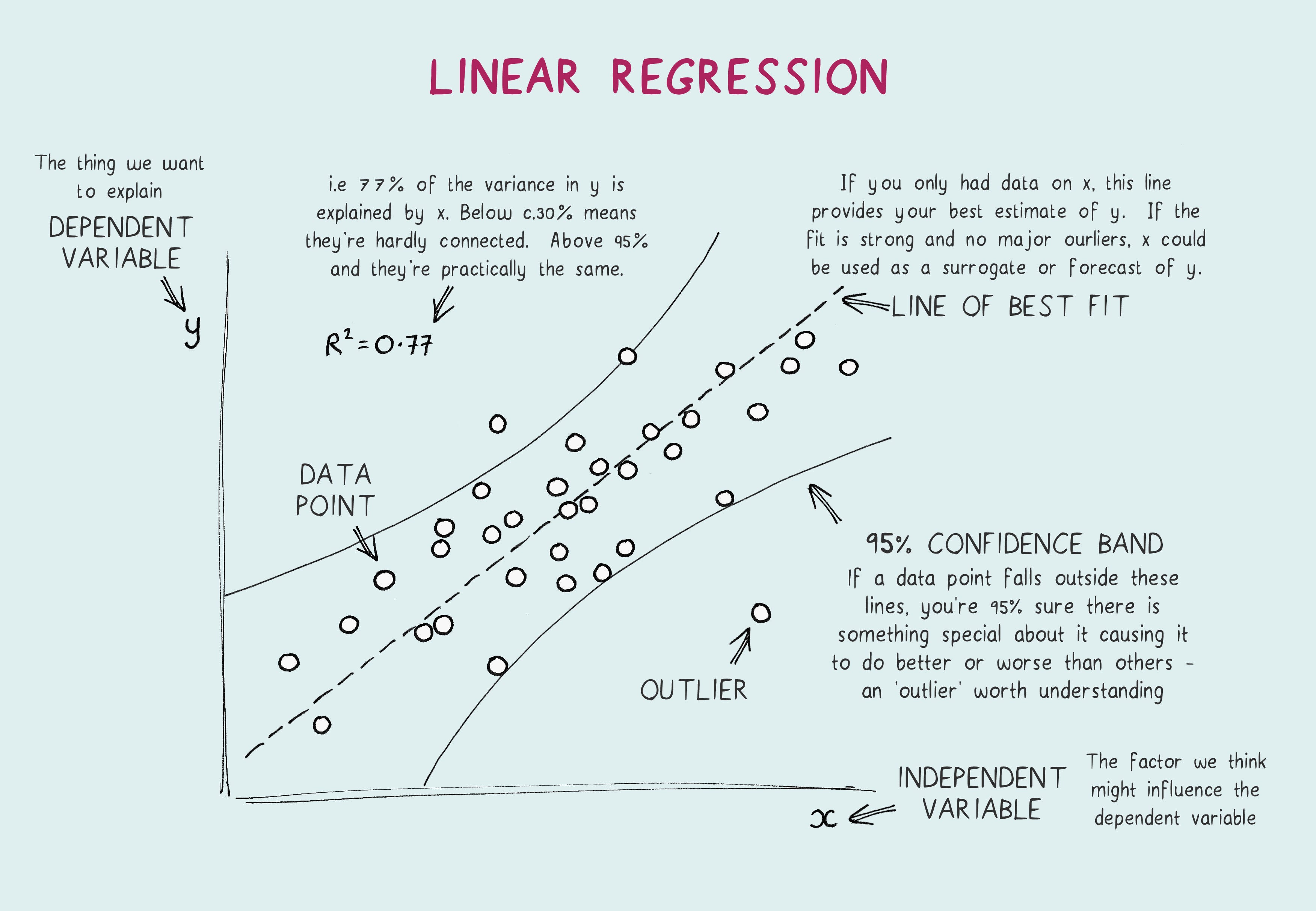
Write down the sample regression function and interpret the coefficient estimates.
- Now estimate the following simple regression model with a level-log specification,
TotalMedals=β0+ β1log(realGDP)+u
Report your regression results in a sample regression function. Interpret the estimated coefficient of log(realGDP). What did you expect this coefficient to be before the estimation and is the sign of this estimate what you expect it to be? Provide an explanation.
- A model that relates the total number of medals to the realGDP and population is:
TotalMedals=β0+ β1realGDP+ β2population+u
Report your results in a sample regression function. What can you conclude regarding comparison of the goodness of fit of this regression model versus the regression model in part (ii)?
- Now re-estimate the equation in (iv) but using the log of independent variables. That is, estimate the model,
TotalMedals=β0+ β1log(realGDP)+ β2log(population)+u
Report the results in a sample regression function. Interpret the coefficient of population. Test whether it is statistically significant at 1% level.
Regression Models Assignment Requirements
- Using the estimated model in (v), test whether realGDP has a positive effect on total medals at 1% level of significance.
- Add the variables planned economy and host country to the level-log equation in (v) and estimate the following model.
TotalMedals=β0+ β1log(realGDP)+ β2log(population)+ β3plannedeconomy+ β4hostcountry+ u
Test whether planned economy variable and host country variables are individually significant at 1% level? Test if plannedeconomy and hostcountry variables are jointly significant at 5% level?
- Test the overall significance of the model you estimated in part (vii) at 1% level of significance.
- Suppose you want to test whether Soviet Union Member countries win more medals than other countries. Specify a regression model that will enable you to test such a hypothesis using the model in (v) as a base. Report your results in a sample regression function and perform the hypothesis test at 5% level of significance. What would you infer?
[3 + 2 + 4 + 4 + 4 + 2 + 4 + 3 + 4 = 30 Marks]



